Listening to equations: a tool for the audification of heteroclinic networks

This story was first published here.

Typically, we are interested in the qualitative long-term behaviour of solutions to differential equations – that is, do the quantities of interest (which might be, for instance, modelling species populations, neural activity, or fluid velocities) eventually settle down to an equilibrium, or do they enter into periodic oscillations, or perhaps become chaotic or blow up to infinity? A heteroclinic cycle is a special type of solution which is associated with intermittent behaviour: the trajectory remains near a state where one species dominates for a time, there is then a rapid change to a state where another species is dominant, and this switching continues forever. In addition, in an idealised context, the switching between states eventually slows down: the period of the oscillations is not constant, but lengthens over time. This can be seen in the time series on Figure 1. Heteroclinic networks are collections of heteroclinic cycles which can be visualised as a directed graph (see Figure 2); here the dynamics can be even more interesting as there are multiple routes around the network that a trajectory might take.

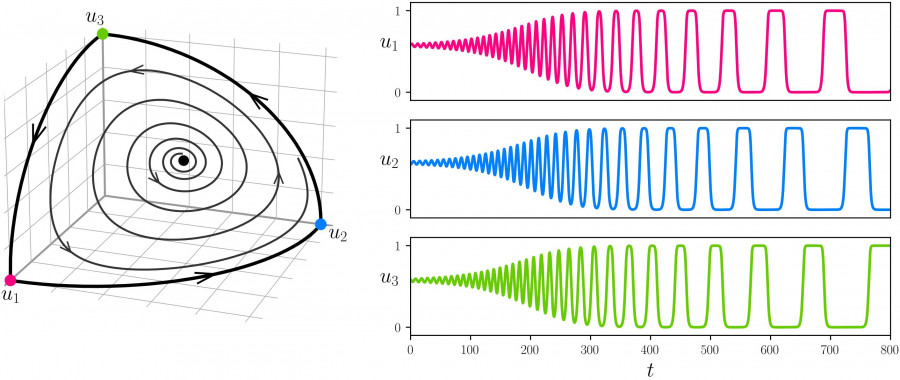
Figure 1. The switching between states eventually slows down: the period of the oscillations is not constant, but lengthens over time. (supplied)

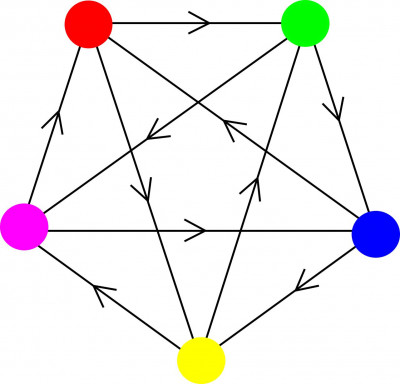
Figure 2. Heteroclinic networks are collections of heteroclinic cycles. (supplied)

Understanding the dynamics near heteroclinic networks is currently an active area of mathematical research, but the focus of the current project is somewhat different. It is possible to view any time series not just as a set of data, but specifically as an audio signal. That is, the amplitude and frequency of the time series can be converted into a sound. The question then becomes, if we do this for a heteroclinic network, what does it sound like? For the simplest heteroclinic network: a heteroclinic cycle, we are able to answer this question rather easily – we can take the time series shown in Figure 1, and directly convert it into an audio signal. Listen below.

The sound of Figure 1.

Because the period of the oscillations in the time-series gradually increases, or in other words, the frequency decreases, the pitch of the sound you hear decreases. Interestingly, it can be shown mathematically that the frequency decreases geometrically with time, and this has the effect that the pitch of the note you hear seems to decrease in a linear fashion: as if you were moving your hand down the notes of a piano at a constant speed. In addition, as time progresses, the oscillations change in shape from sinusoidal to square waves; this causes the change in timbre you can hear from the pure tone of the sinusoidal to the harsher sound of the square wave.  

Heteroclinic networks have more complex dynamics than heteroclinic cycles, and thus also more complex time series. Trajectories near the network shown in Figure 2, which has five states, can demonstrate switching between different cycles. For instance, a trajectory might oscillate between the green, blue and yellow states for some time, and then switch to the blue, yellow and pink states. Because different states are active at different times, we can create multiple audio channels (one for each state) to create stereo sounds (this stereo file is best experience with headphones) to an example. ​

The sound of Figure 2.

The pitch again decreases, but not so steadily; there are discontinuous jumps in both volume and pitch as the trajectory switches between different parts of the network.

The audio files linked to above are both generated using a single set of parameters, and each only demonstrate one of many different possible types of behaviour. In collaboration with Nelis Drost at the Centre for eResearch, we have been developing an interactive piece of software which allows the user to interact with the dynamics of the heteroclinic network in an audible fashion. This includes active variation of parameters, and addition of user inputs to the system. The software includes a GUI designed to allow the user to intuitively select parameter values to listen to, and interactively explore the system. Click here. There have been several technical challenges, the primary one being producing a computational solution to the system of equations fast enough to listen to the result as audio playback.

This was resolved by using the Julia language, which has a library of particularly fast numerical solvers. Secondary to this, the software needed to feel responsive to the user, with minimal latency between the selection of new parameters and an audible change in the system, but without gaps in the output. This required careful design of a system for buffering the integration result, allowing this buffer to be discarded and replaced on new parameter selection, and fine tuning of how much of that buffer is kept. Going forward, I’m interested in further exploring the sonic space associated with these sorts of equations, and potentially using the software developed here to bring this work to a larger audience.

Additional information: Link to the original article